Dynamical systems can exhibit geometrically rich behavior, due in part to the uniqueness of solutions to ODEs.
Under certain conditions, some systems remain confined to a finite subset of Euclidean space. Since the trajectories extend infinitely in time,
they form infinitely long parametric curves in 3D space that remain within this bounded region. Because the trajectories are unique,
they can never intersect at any point in time. As a result, each curve must weave around every other possible trajectory infinitely,
yet still remain within the confined space. This behavior gives rise to the videos and some of the images of the systems shown below.
The videos below were rendered offline with my 3D phase space simulation.
The online version does not include a screen recording feature but does support taking screenshots.
Lorenz Attractor
Dequan Li Attractor
Chen Lee Attractor
Aizawa Strange Attractor
Three-Scroll Attractor
Halvorsen System
Newton-Leipnik System
Rössler System
Aizawa attractor visualization from my 3D phase space simulation


3D Lorenz System visualization from my 3D phase space simulation
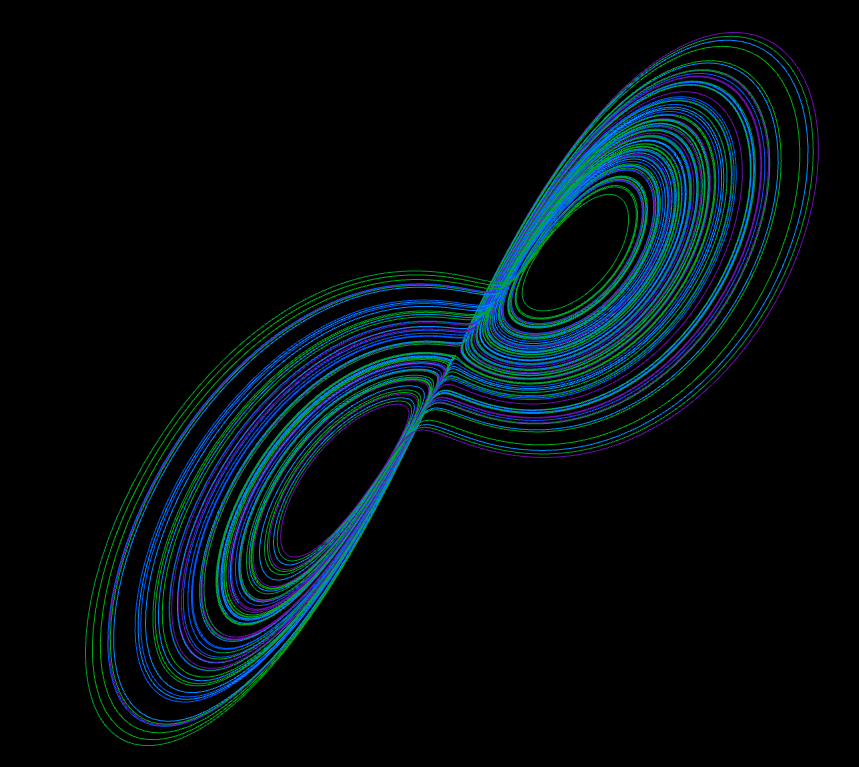

Halvorsen System from my 3D phase space simulation
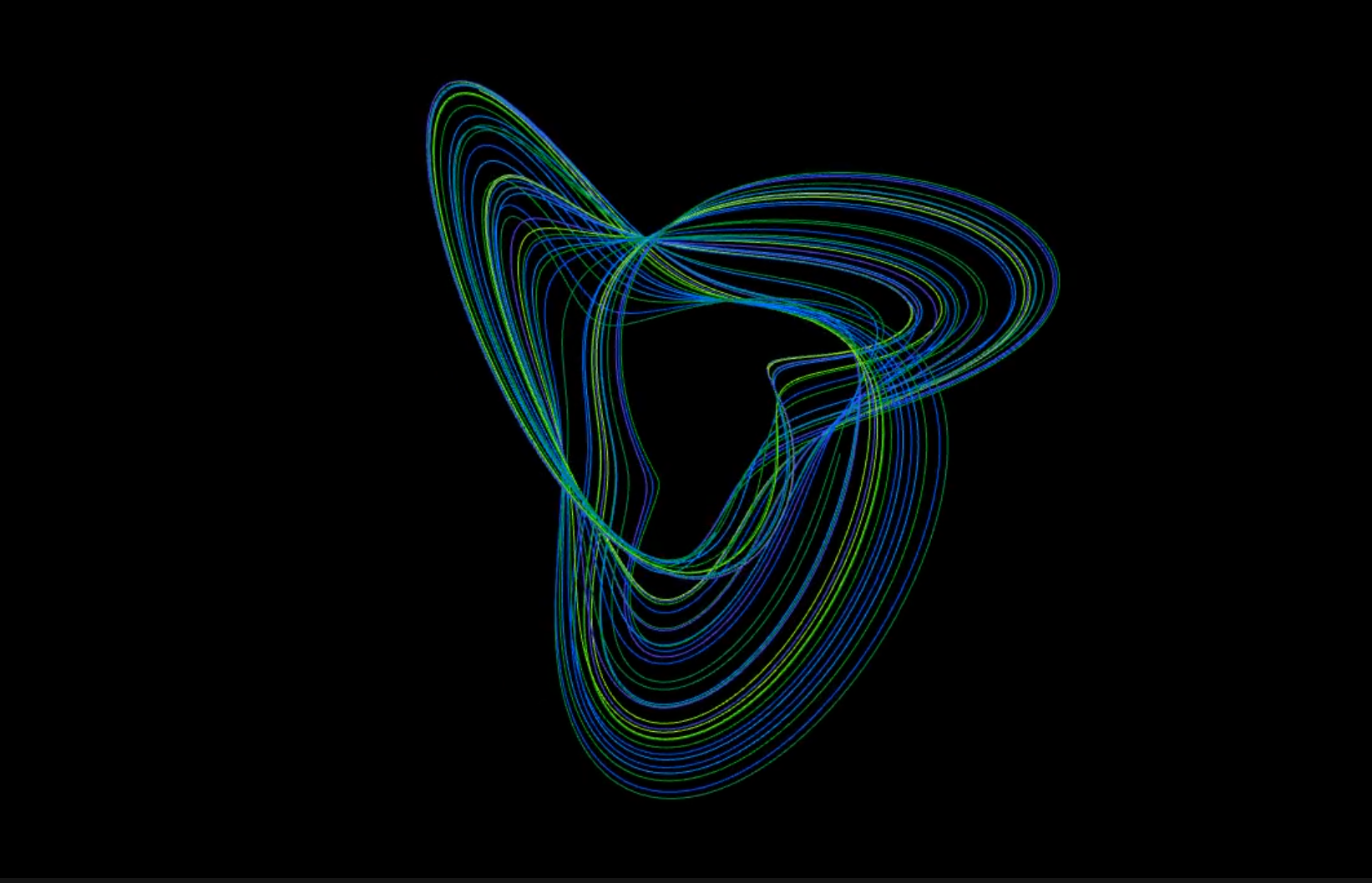

Aizawa attractor from another point of view, from: 3D phase space simulation


Another 3D Lorenz System visualization from my 3D phase space simulation


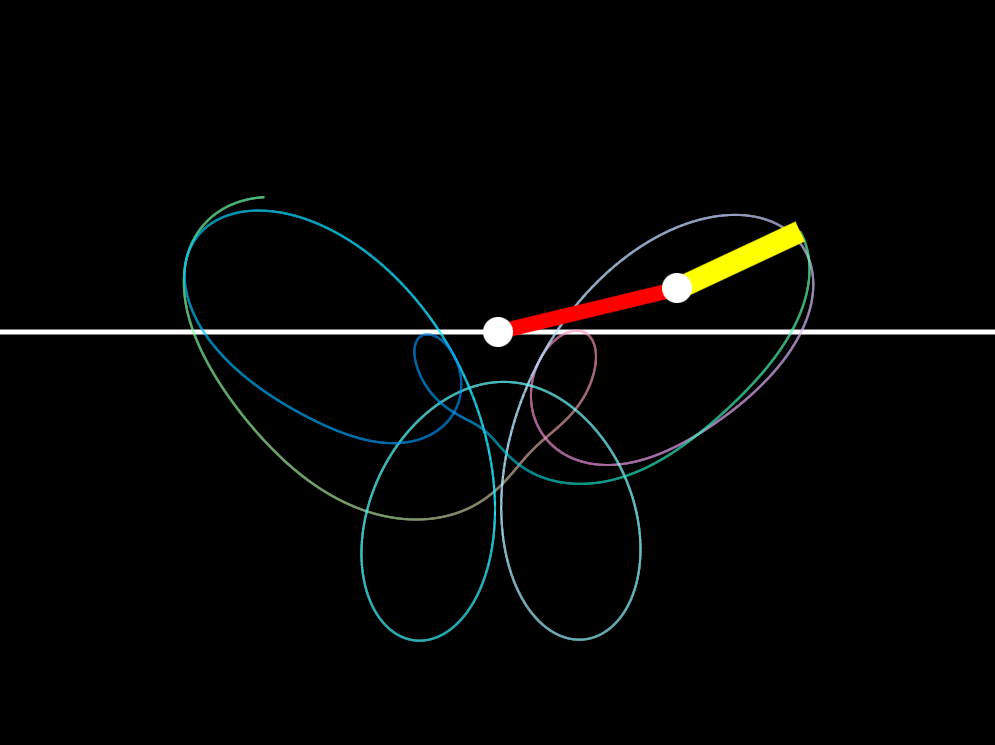
Butterfly shaped curve drawn by my chaotic double pendulum simulation

Heart drawn by my chaotic double pendulum simulation


Fox-like 3D parametric curve visualized in 2D, produced by
altering the normal coefficients of the Lorenz system.
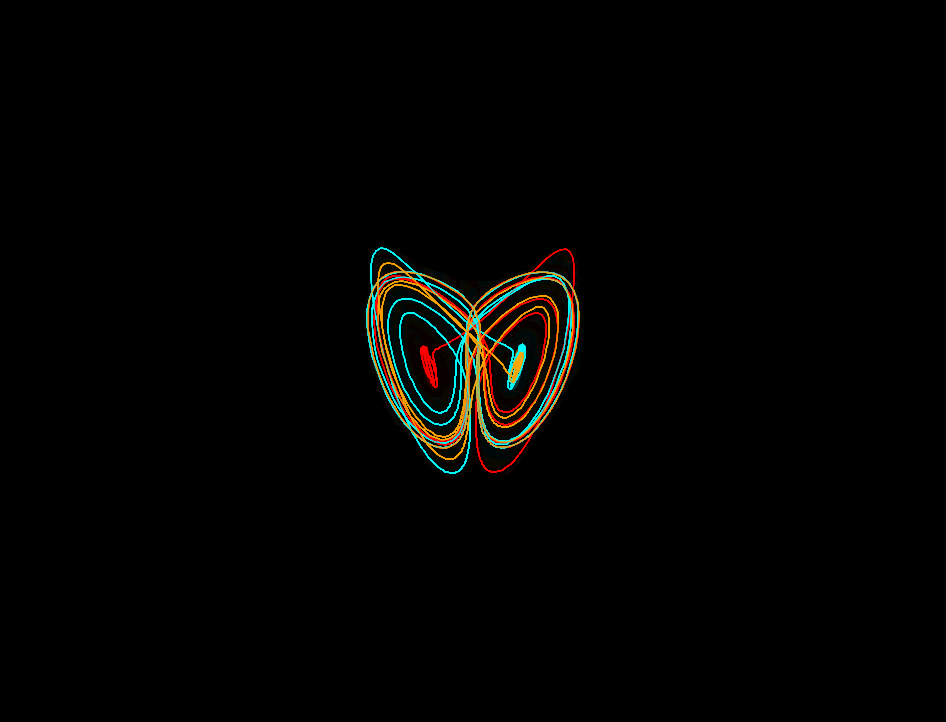
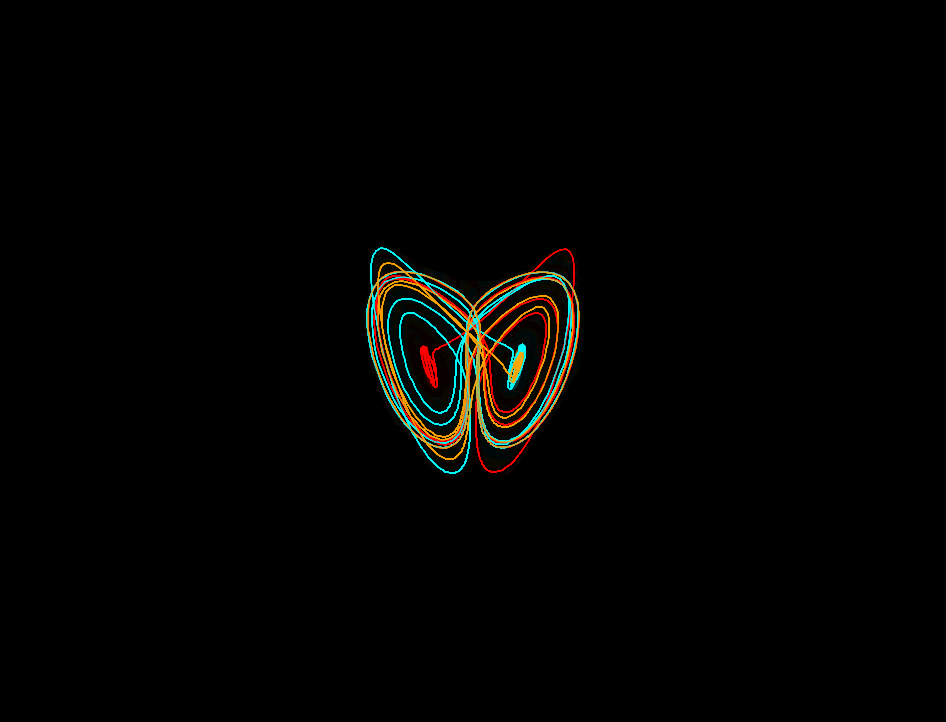
Flower shape generated by Jupiter's moon's orbit path, produced by n-Body Simulation

Classic 2D visualization of Lorenz system with normal and constant
coefficients. Three trajectories (orange, blue, and red), are started within
0.001 of each other, yet very different trajectories are formed.
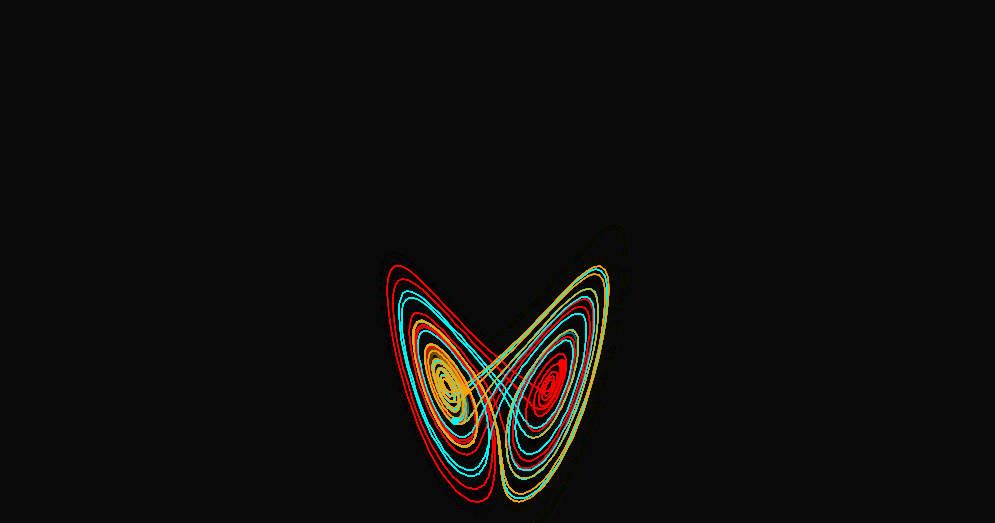
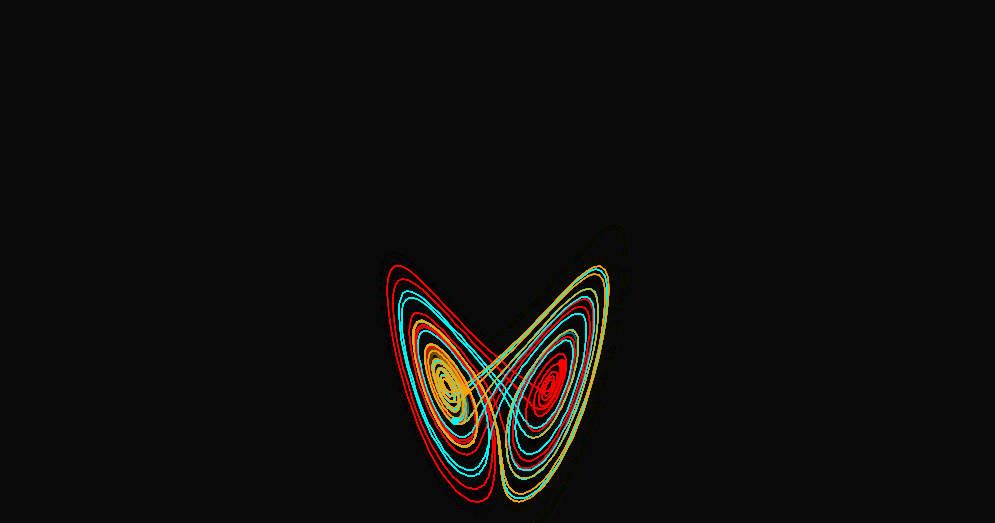
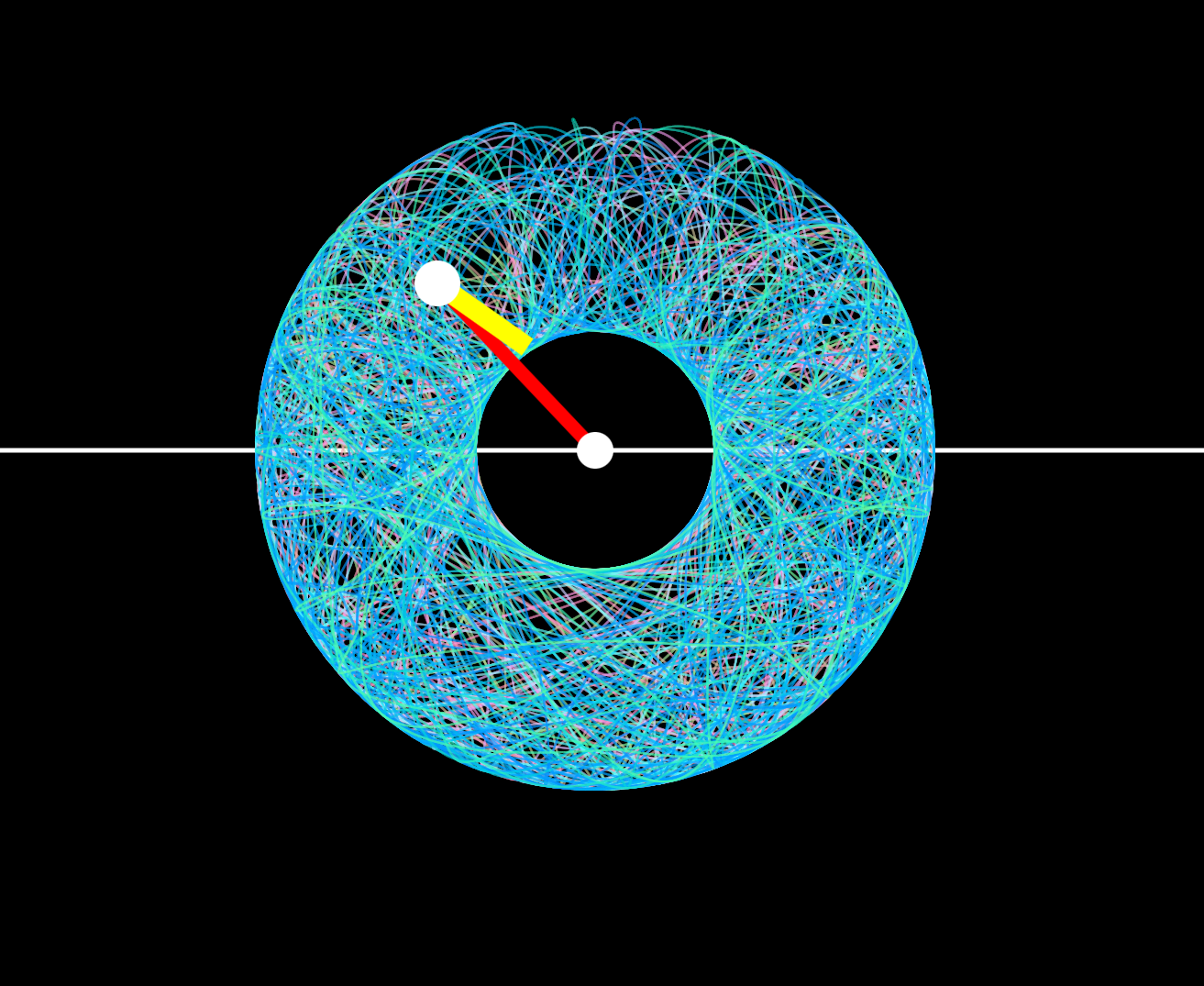
Torus drawn out by my chaotic double pendulum simulation

Chemical concentration of two reactive chemicals, generated by my simulation: Turing Patterns


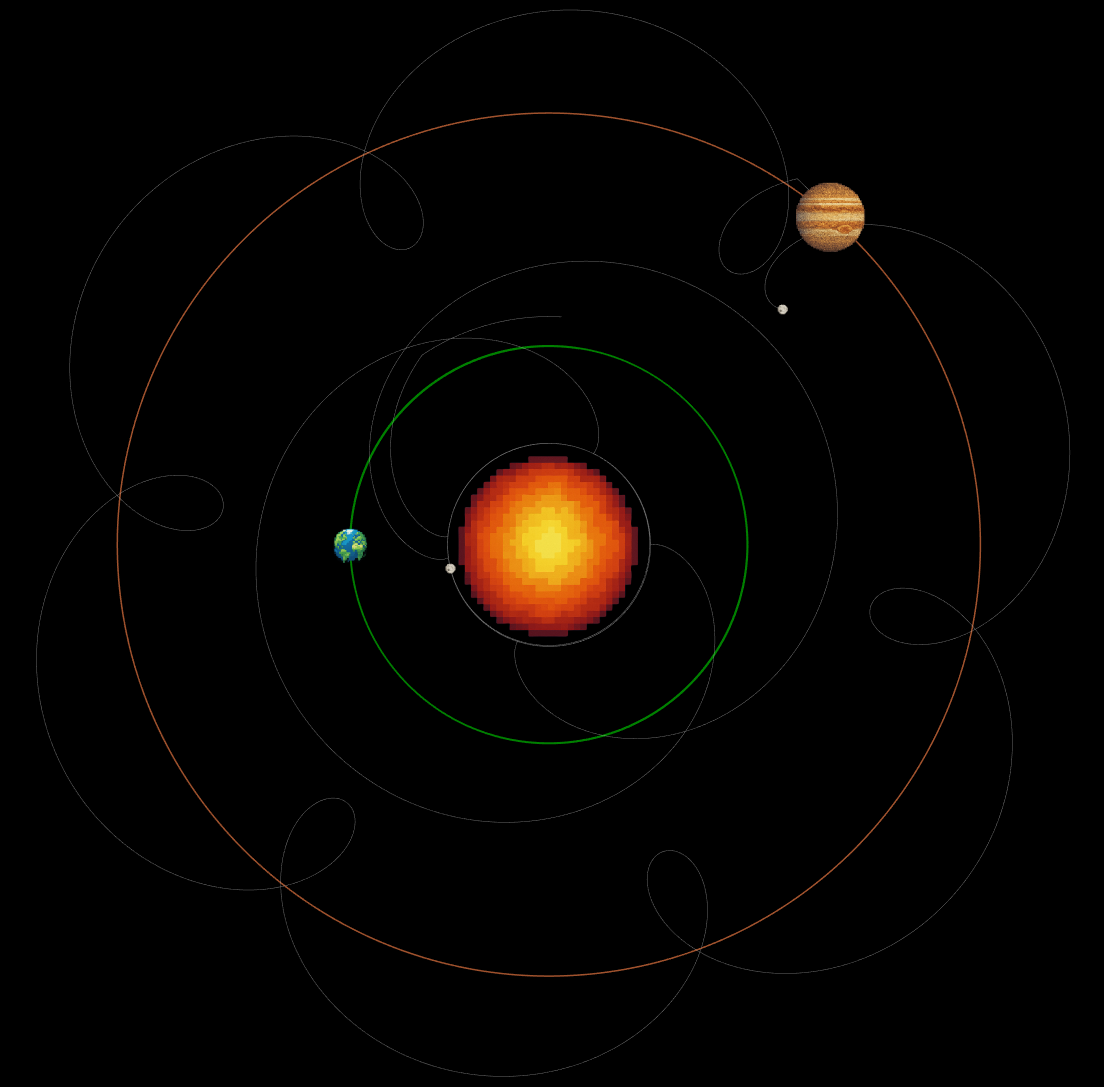
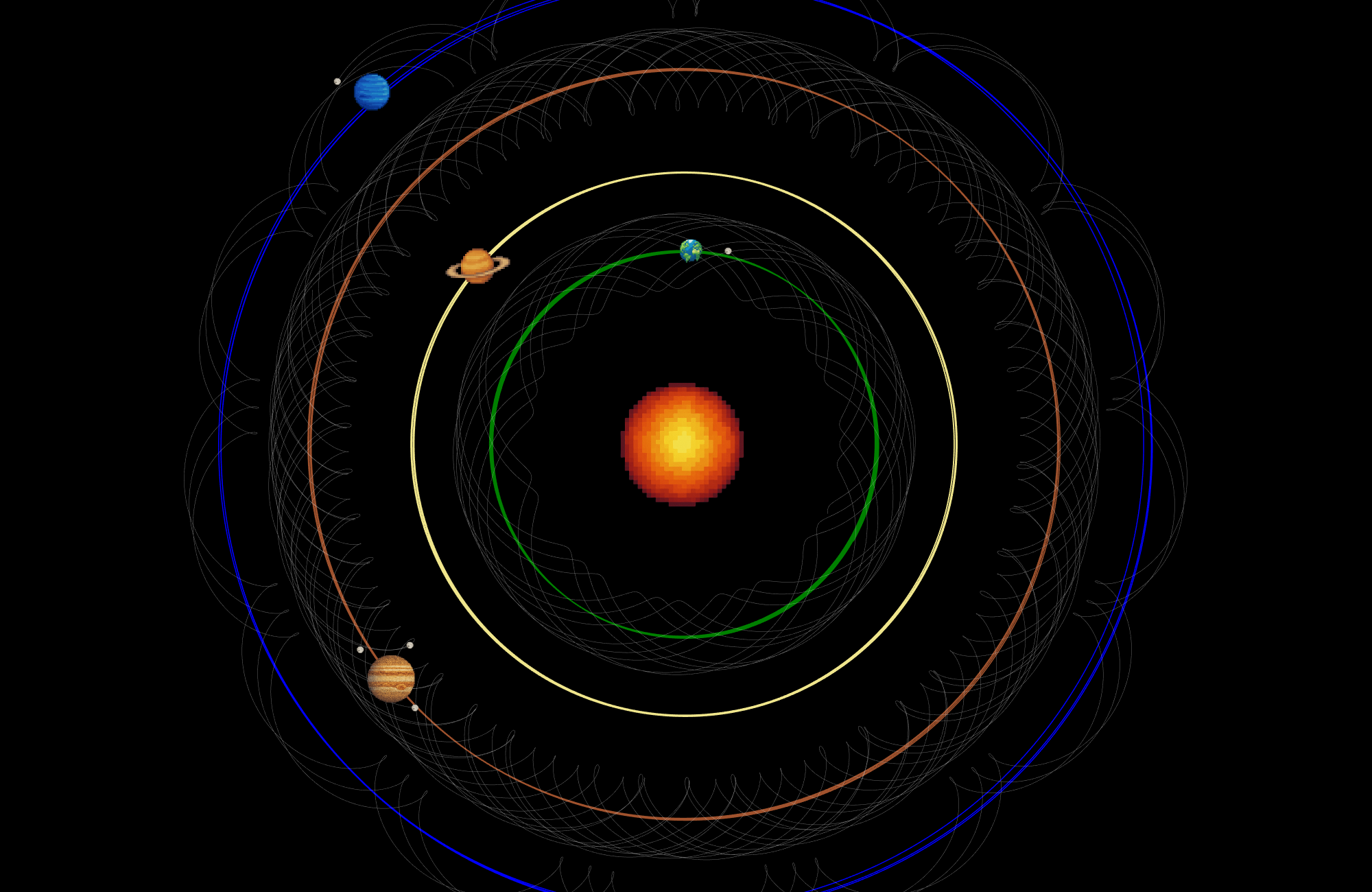
Cool looking solar system generated by, n-Body Simulation

Lorenz Attractor with large orbital amplitudes


Small butterfly
Cat-like mask


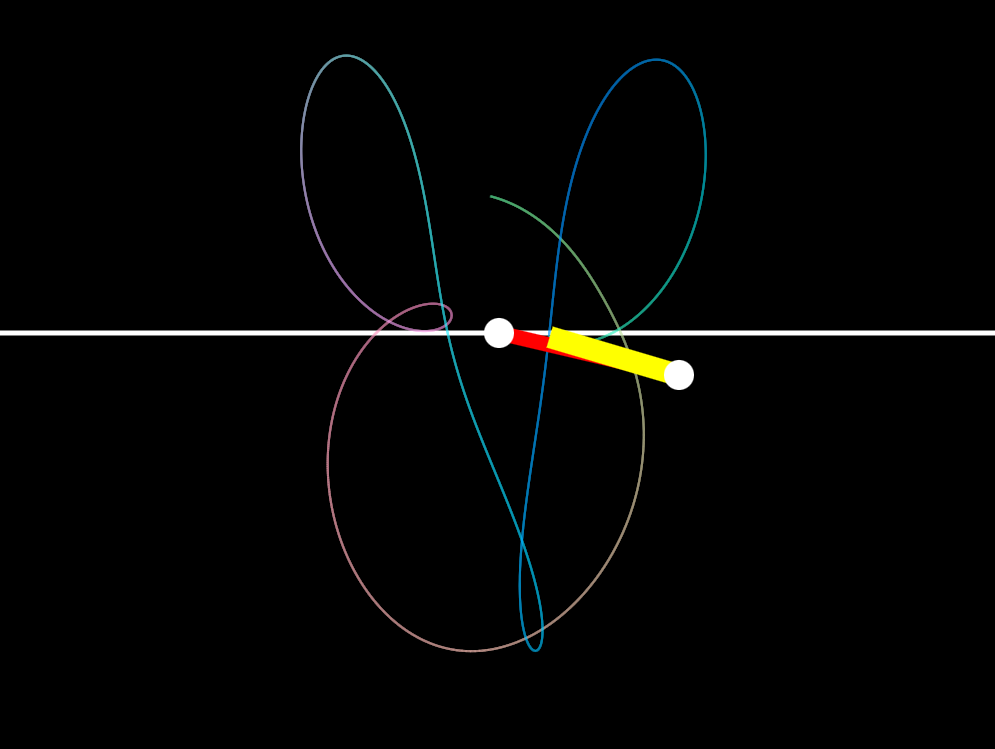
Rabbit drawn by my chaotic double pendulum simulation